zurück zum Index

Quantum States und Qubits

Single Qubit Gates

import numpy as np

# Importing standard Qiskit libraries
from qiskit import QuantumCircuit, transpile, Aer, IBMQ
from qiskit.tools.jupyter import *
from qiskit.visualization import *
from ibm_quantum_widgets import *
from qiskit.providers.aer import QasmSimulator

# Loading your IBM Quantum account(s)
provider = IBMQ.load_account()

ibmqfactory.load_account:WARNING:2023-03-06 17:12:31,838: Credentials are already in use. The existing account in the session will be replaced.

Import Basic Functions First

import qiskit
from qiskit import ClassicalRegister, QuantumRegister, QuantumCircuit
from qiskit import execute, BasicAer, Aer
from qiskit.tools.visualization import plot_histogram, circuit_drawer

from qiskit.visualization import plot_state_qsphere
from qiskit.visualization import plot_bloch_multivector, array_to_latex
from numpy import sqrt, pi

Das X-Gate

Das Pauli-X-Gatter ist eine Ein-Qubit-Drehung durch π Radiant um die x-Achse.

X	0> =	1>
X	1> =	0>

Let’s do an X-gate on a qubit 0: |0> qubit

qc = QuantumCircuit(1)
qc.x(0)
qc.draw()

Schauen wir uns das Ergebnis der obigen Schaltung an. Hier verwenden wir plot_bloch_multivector(), das den Zustandsvektor eines Qubits anstelle des Bloch-Vektors nimmt.

backend = BasicAer.get_backend('statevector_simulator')
job = execute(qc, backend).result()
plot_bloch_multivector(job.get_statevector(qc), title='X-Gate')

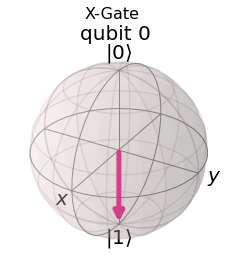
Wir können sehen, dass der Zustand des Qubits |1> tatsächlich wie erwartet ist. Wir können uns dies als eine Drehung im Bogenmaß π um die x-Achse der Bloch-Kugel vorstellen. Das X-Gate wird in Anlehnung an sein klassisches Analogon oft auch als NOT-Gate bezeichnet.

Das Y-Gate

Das Pauli-Y-Gatter ist eine Ein-Qubit-Drehung durch π um die y-Achse

qc = QuantumCircuit(1)
qc.y(0) # Do Y-gate on qubit 0
qc.draw()

backend = BasicAer.get_backend('statevector_simulator')
job = execute(qc, backend).result()
plot_bloch_multivector(job.get_statevector(qc), title='Y-Gate')

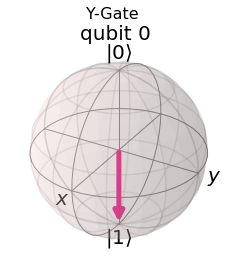
Das Z-Gate

Das Pauli-Z-Gatter ist eine Ein-Qubit-Drehung durch π um die z-Achse

qc = QuantumCircuit(1)
qc.z(0) # Do Z-gate on qubit 0
qc.draw()

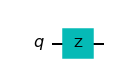
backend = BasicAer.get_backend('statevector_simulator')
job = execute(qc, backend).result()
plot_bloch_multivector(job.get_statevector(qc), title='Z-Gate')

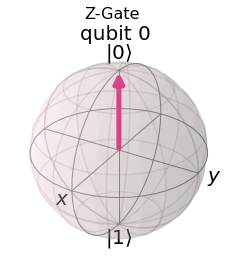
Unten sehen Sie ein Widget, das den Zustand eines Qubits auf der Bloch-Kugel anzeigt. Wenn Sie einen der Knöpfe drücken, wird das Gate auf dem Qubit ausgeführt:

# Run the code in this cell to see the widget
from qiskit_textbook.widgets import gate_demo
gate_demo(gates='pauli')

HBox(children=(Button(description='X', layout=Layout(height='3em', width='3em'), style=ButtonStyle()), Button(…



Image(value=b'\x89PNG\r\n\x1a\n\x00\x00\x00\rIHDR\x00\x00\x01 \x00\x00\x01 \x08\x06\x00\x00\x00\x14\x83\xae\x8…

Das Hadamard Gate

Das Hadamard-Gate (H-gate) ist ein grundlegendes Quantengate. Es erlaubt, sich von den Polen der Bloch-Sphäre zu entfernen und eine Überlagerung von

0⟩ und

1⟩

Es werden dadurch die folgenden Transformationen durchgeführt:

H	0⟩=	+⟩
H	1⟩=	−⟩

Dies kann man sich als eine Drehung um den Bloch-Vektor [1,0,1] (die Linie zwischen der x- und der z-Achse) vorstellen, oder als eine Transformation des Zustands des Qubits zwischen der X- und der Z-Basis.

Mit dem untenstehenden Widget lässt sich mit diesen Gates experimentieren:

# Run the code in this cell to see the widget
from qiskit_textbook.widgets import gate_demo
gate_demo(gates='pauli+h')

HBox(children=(Button(description='X', layout=Layout(height='3em', width='3em'), style=ButtonStyle()), Button(…



Image(value=b'\x89PNG\r\n\x1a\n\x00\x00\x00\rIHDR\x00\x00\x01 \x00\x00\x01 \x08\x06\x00\x00\x00\x14\x83\xae\x8…

QuantumCircuit (4, 3)

Ein QuantumCircuit mit 4 qubits und 3 klassischen Bits

https://qiskit.org/documentation/stubs/qiskit.circuit.QuantumCircuit.html