#

zurück zum Index

Einen Quantencomputer programmieren

Einen Quantencomputer zu programmieren, kann jetzt jeder bequem von zu Hause aus tun. Aber was soll man programmieren? Was ist überhaupt ein Quantenprogramm? Und was ist eigentlich ein Quantencomputer?

Diese Fragen lassen sich durch Vergleiche mit herkömmlichen digitalen Computern beantworten. Leider wissen die meisten Menschen auch nicht, wie herkömmliche Digitalcomputer funktionieren. Auf dieser Seite werden wir uns mit den grundlegenden Prinzipien dieser traditionellen Geräte befassen. Um uns später den Übergang zum Quantencomputer zu erleichtern, werden wir die gleichen Werkzeuge verwenden, die wir auch für Quantencomputer einsetzen.

Quanten Schaltkreise bzw Diagramme

Eine Berechnung benötigt einige Eingabedaten und Operationen, die darauf ausführt werden, um Ausgabedaten zu erzeugen. Bei den Quantencomputern, liegen diese Daten immer in Form von Bits vor.

Es ist oft nützlich, diesen Prozess in einem Diagramm darzustellen, das als Schaltplan bekannt ist. Diese Diagramme haben Eingänge auf der linken Seite, Ausgänge auf der rechten Seite und dazwischen Operationen, die durch Gatter-Symbole dargestellt werden. Diese Operationen werden “Gatter” genannt, meist aus historischen Gründen. Hier ist ein Beispiel dafür, wie ein Schaltkreis für Standard-Bitcomputer aussieht.

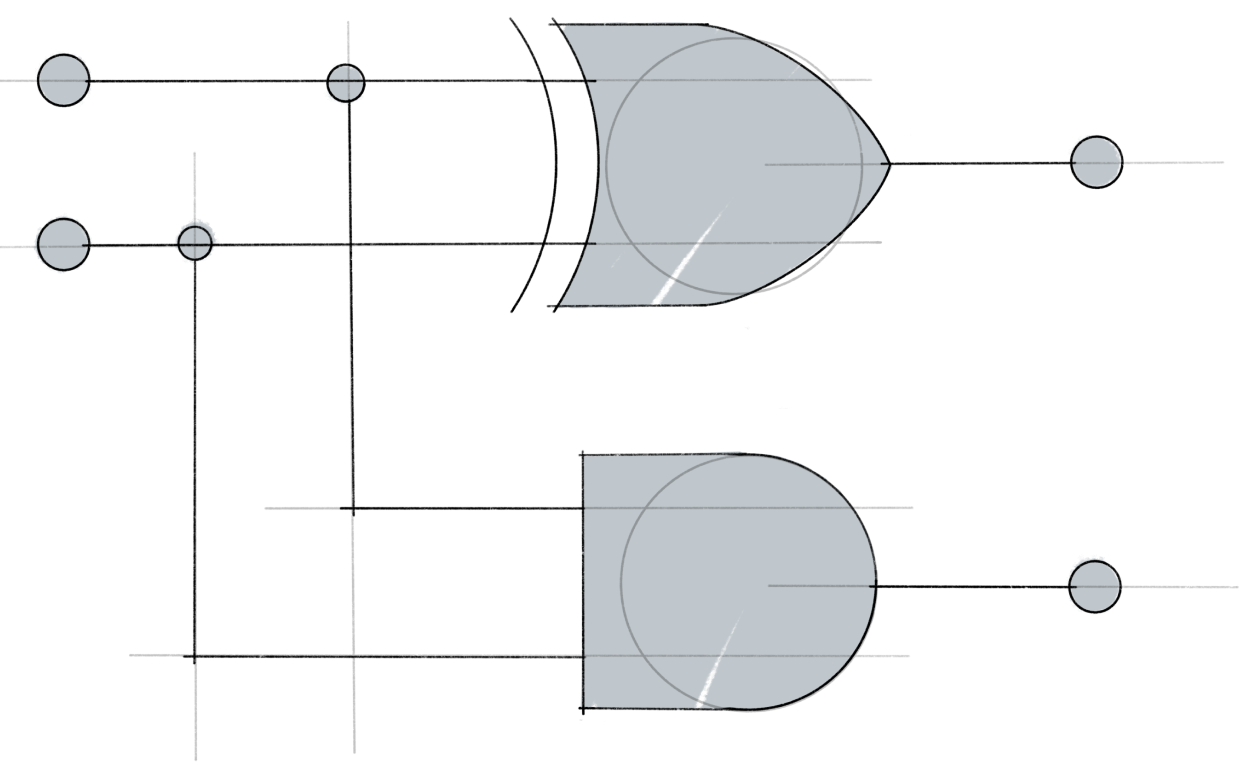
Es wird nicht von Ihnen erwartet, dass Sie verstehen, was sie tut. Es soll Ihnen lediglich eine Vorstellung davon vermitteln, wie diese Schaltungen aussehen.

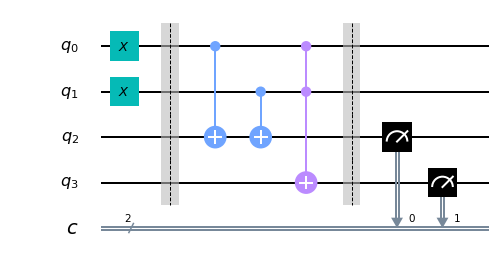
Bei Quantencomputern verwenden wir dieselbe Grundidee, haben aber andere Konventionen für die Darstellung von Eingängen, Ausgängen und den für Operationen verwendeten Symbolen. Hier ist die “Quantenschaltung”, die den gleichen Prozess wie oben darstellt.

Quantum Computer programmieren mit Qiskit

Das Hauptziel von Qiskit ist es, einen Software-Stack zu entwickeln, der es jedem leicht macht, Quantencomputer zu benutzen, unabhängig von seinen Fähigkeiten oder seinem Interessengebiet; Qiskit ermöglicht es, Experimente und Anwendungen einfach zu entwerfen und sie auf echten Quantencomputern und/oder klassischen Simulatoren auszuführen. Qiskit wird bereits auf der ganzen Welt von Anfängern, Bastlern, Lehrern, Forschern und kommerziellen Unternehmen genutzt.

Schaltkreise mit Qiskit erstellen

Basics

Wir wissen, dass wir alle Informationen mit einem Bündel von Bits beschreiben können. So speichern und verarbeiten Computer alles, auch Quantenschaltungen! Aber für uns Menschen ist es schwierig, darüber nachzudenken, wie wir dies tun und wie wir diese Bits manipulieren, um die gewünschten Schaltungen darzustellen.

Ein “QuantumCircuit” ist ein Satz von Anweisungen zur Darstellung von Quantenschaltungen als Bits. Die Zeile

qc = QuantumCircuit(4, 2) 

ist ein Konstruktor, der Python anweist, einige Bits in Ihrem Computer bereitzustellen, die wir zur Darstellung eines Quantenschaltkreises verwenden werden. Wenn wir uns auf diesen Quantenschaltkreis beziehen wollen (oder besser gesagt, auf die Bits, die diesen Quantenschaltkreis darstellen), verwenden wir die Variable “qc”.

Wir sagen, dass sich ‘qc’ auf ein “QuantumCircuit-Objekt” bezieht.

Dies ermöglicht es uns Menschen, über Quantenschaltungen auf einer hohen, abstrakten Ebene nachzudenken; wir können Anweisungen wie “füge ein X-Gate hinzu” und Qiskit kümmert sich darum, was wir mit den Bits in unserem Computer machen müssen, um diese Änderung zu reflektieren.

Um einen Quantenschaltkreis zu erstellen, importieren wir die Klasse QuantumCircuit und erstellen ein neues QuantumCircuit-Objekt.

Wenn wir einen Quantenschaltkreis erstellen, müssen wir Python (Python ist eine Programmiersprache. Mit ihr können wir Anweisungen und Algorithmen schreiben, denen Computer folgen können.)

sagen, wie viele Qubits unsere Schaltung haben soll, und wir können ihr optional auch mitteilen, wie viele klassische Bits unsere Schaltung haben soll. Wir brauchen klassische Bits, um die Messungen unserer Qubits zu speichern.

Quiskit MyFirstSample für Quantenschaltkreise (Gates)

Quiskit Erste Beispiele für Quantenschaltkreise (Gates)

Codierung einer Eingabe

Schauen wir uns nun an, wie man eine andere binäre Zeichenfolge als Eingabe kodieren kann. Dazu benötigen wir ein sogenanntes NOT-Gatter. Dies ist die einfachste Operation, die man in einem Computer durchführen kann. Dabei wird der Bitwert einfach umgedreht: 0 wird zu 1 und 1 wird zu 0. Bei Qubits verwenden wir dafür ein so genanntes X-Gatter.

Im Folgenden werden wir eine neue Schaltung erstellen, die sich mit der Kodierung befasst:

# Create quantum circuit with 3 qubits and 3 classical bits:
qc = QuantumCircuit(3, 3)
qc.x([0,1])  # Perform X-gates on qubits 0 & 1
qc.measure([0,1,2], [0,1,2])
qc.draw()    # returns a drawing of the circuit

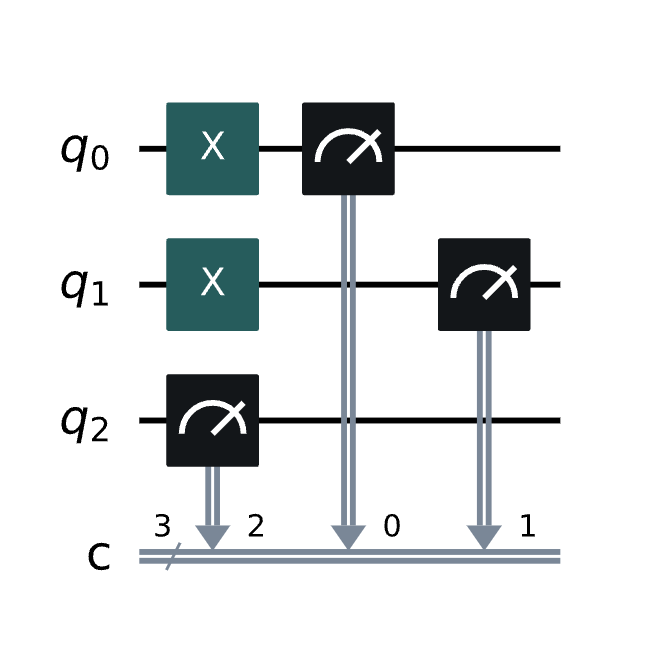
Und die Simulation unserer Schaltung, um die Ergebnisse zu sehen:

job = sim.run(qc)      # run the experiment
result = job.result()  # get the results
result.get_counts()    # interpret the results as a "counts" dictionary

Result:

{'011': 1024}

Quick quiz Wie lautet die Binärzahl 011 in Dezimalzahlen?

A: 2 B: 5 C: 3

Ändern Sie den obigen Code, um eine Quantenschaltung zu erstellen, die die Zahlen 6 und 4 kodiert. Sind die Ergebnisse so, wie Sie sie erwarten?

Lösung: C

Jetzt wissen wir, wie man Informationen in einem Computer kodiert.

Der nächste Schritt besteht darin, sie zu verarbeiten: Wir nehmen eine Eingabe, die wir kodiert haben, und verwandeln sie in eine Ausgabe, die uns etwas Neues sagt.

Erstellen einer Additionsschaltung

Lassen Sie uns ein paar grundlegende mathematische Berechnungen durchführen.

Grosse mathematische Probleme werden zunächst in überschaubare Teilaufgaben zerlegt.

Wie würdest du zum Beispiel dieses Additionsproblem lösen?

Um auf einem Computer laufen zu können, müssen die Algorithmen in die kleinstmöglichen und einfachsten Schritte zerlegt werden. Um zu sehen, wie diese aussehen, wiederholen wir das obige Additionsproblem, aber in binärer Form.

Addieren mit Quantum Circuits

Wir wollen unseren eigenen “Halb-Addierer” aus einer Quantenschaltung bauen. Dazu gehört ein Teil der Schaltung, der die Eingabe kodiert, ein Teil der den Algorithmus ausführt, und einen Teil, der das Ergebnis extrahiert. Der erste Teil muss geändert werden, wenn wir eine neue Eingabe verwenden wollen, aber der Rest wird immer gleich bleiben.

Die beiden Bits, die wir addieren wollen, sind in den Qubits 0 und 1 kodiert. Das obige Beispiel kodiert eine 1 in diesen beiden Qubits und versucht daher, die Lösung 1+1 zu finden. Das Ergebnis ist eine Folge von zwei Bits, die wir aus den Qubits 2 und 3 ablesen. Jetzt muss nur noch das eigentliche Programm ausgefüllt werden, das sich in dem leeren Raum in der Mitte befindet.

Die gestrichelten Linien in der Abbildung dienen nur dazu, die verschiedenen Teile des Schaltkreises zu unterscheiden (obwohl sie auch interessantere Verwendungen haben können)

Die Grundoperationen des Rechnens sind als logische Gatter bekannt. Wir haben bereits das NOT-Gatter verwendet, aber das hilft uns in diesem Beispiel nicht weiter. Da wir wollen, dass der Computer die eigentliche Rechenarbeit für uns erledigt, brauchen wir einige leistungsfähigere Gatter.

Um zu sehen, was wir brauchen, sehen wir uns noch einmal an, was unser “Halbaddierer” tun muss.

Um diesen Teil unserer Lösung richtig zu machen, brauchen wir etwas, das herausfinden kann, ob zwei Bits unterschiedlich sind oder nicht. Im Studium der digitalen Berechnungen wird dies traditionell als XOR-Gatter bezeichnet.

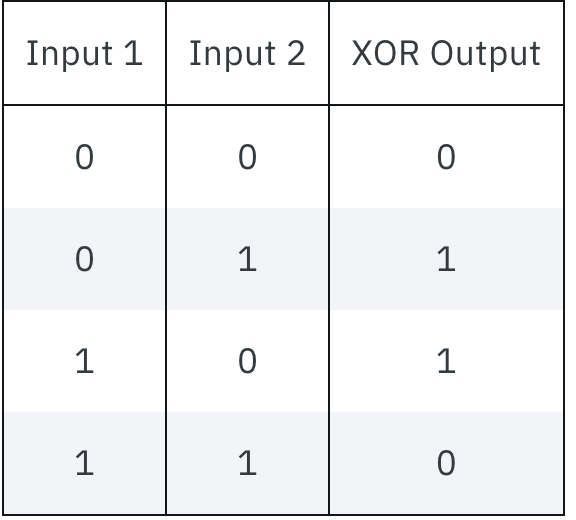
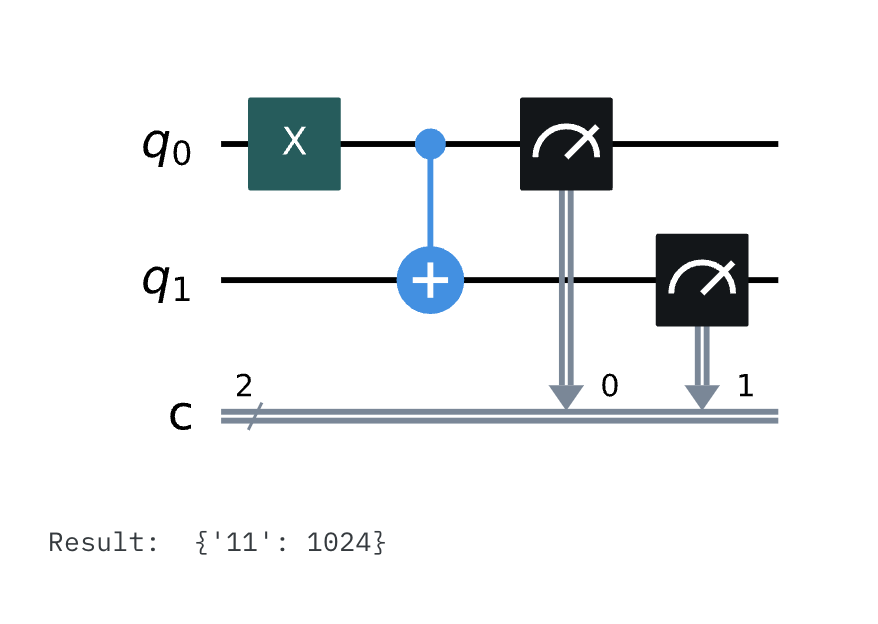
In Quantencomputern wird die Aufgabe des XOR-Gatters durch das “controlled-NOT-Gatter” übernommen. Da das ein ziemlich langer Name ist, nennen wir es gewöhnlich einfach “CNOT”. In Schaltplänen wird es wie in der Abbildung unten dargestellt. Es wird auf ein Paar Qubits angewendet. Das eine fungiert als Kontroll-Qubit (das ist das mit dem kleinen Punkt). Das andere fungiert als Ziel-Qubit (mit dem großen Kreis und dem Kreuz - eine Art Zielmarkierung).

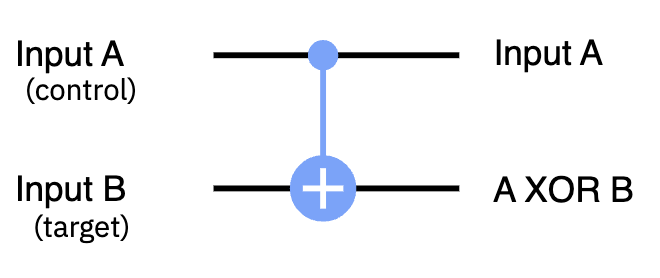
In Qiskit können wir die Methode .cx() verwenden, um einen CNOT zu unserer Schaltung hinzuzufügen. Wir müssen die Indizes der beiden Qubits, auf die es wirkt, als Argumente angeben. Hier ist ein Beispiel:

# Create quantum circuit with 2 qubits and 2 classical bits
qc = QuantumCircuit(2, 2)
qc.x(0)
qc.cx(0,1)  # CNOT controlled by qubit 0 and targeting qubit 1
qc.measure([0,1], [0,1])
display(qc.draw())     # display a drawing of the circuit

job = sim.run(qc)      # run the experiment
result = job.result()  # get the results
# interpret the results as a "counts" dictionary
print("Result: ", result.get_counts())